I’m working on a text on computational physics whose primary goal is to create something useful for a one semester introductory course that all our physics majors (and now chemistry majors too) will be required to take. I want students to come away with tools that they’ll use later in their student careers (undergraduate & graduate) and can use for their professional work as well. The toolkit that I want them to develop includes: being able to use LaTeX, read data files, plot and fit data, as well as the standard fare of creating simulations to learn about physical systems. After taking this class, my hope is that they will naturally turn to python/numpy/matplotlib to process & visualize their data, and know the limitations of these tools, and where to go if these limits are exceeded.
I’m realizing that this toolkit portion is more important than I’ve previously thought — when you’re in the laboratory taking data, you’ve got to analyze it, make plots, & write about your work—-these are skills that ALL scientists need, all the time, and it’s making me rethink my course as part 1 of an eventual two semester sequence, and this also changes the way I think about the text.
So, in an effort to grab the attention of the non-physicists in my course, I thought I’d work on including (early on, rather than waiting several weeks or months) something basic that all science students need to be able to do—read a data file, filter out bad data, and visualize the data. The data set I chose to work with is the weather data from the summit of Mt. Washington, NH, the highest peak in New England, and home to some surprisingly bad weather like 231mph wind speeds.
I obtained the data from NOAA Climatic Data Center. I used “go to map application” button and retrieve a comma-separated-value (.csv file) that looked like this
USAF, NCDC, Date, HrMn,I,Type,Dir, Q,I, Spd,Q, Temp, Q,
726130,14755,20060101,0059,7,FM-15,240,1,N, 1.0,1, -8.0,1,
726130,14755,20060101,0159,7,FM-15,180,1,N, 2.1,1, -8.0,1, …..
etc. For about 250,000 lines — as I downloaded the weather data from 1973 to 2013. Notice that that data didn’t start from 1973. For some bizarre reason it was in a few contiguous, but out of order blocks. The columns I’m interested in here are Date, HrMn, Dir, Spd, and Temp (when you get the download link from NOAA after requesting the data, the download includes a descriptor file that details what’s in each column. Navigating the NOAA site to finally choose and request a download link to the datais a post in itself. )
So there we are—the data’s in front of me on my hard disk, but to see it and analyze it, I need to read it, combine the date-time data, sort it in time, extract the columns I want, eliminate the bogus data points (they were set to either 999 or 999.9 in the raw data file) and finally plot it. Turns out 250,000 points is too much for matplotlib to deal with gracefully unless you plot it within an iPython notebook (at least on OS X); more about that later.
Part 2 will show how to obtain this plot:

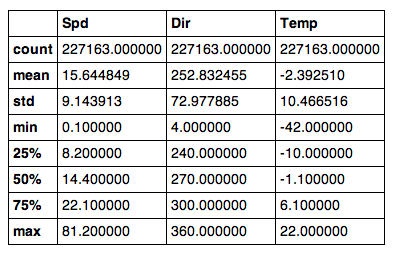
and this summary via Python & Pandas (notice the minimum temperature of -42 C, and the maximum wind speed of 81.2 m/s (or 182 mph for the metrically disinclined):
Just for fun, here’s a plot of the Wind Speed versus the temperature:

and, interestingly, here’s a plot of the temperature vs the north component of the wind speed (positive = north, negative =south). Curiously, it seems symmetrical about the N-S direction, which surprises me: